Matemáticas

La matemática en realidad es un conjunto de lenguajes formales que pueden ser usados como herramienta para plantear problemas de manera no ambigua en contextos específicos. Por ejemplo, el siguiente enunciado podemos decirlo de dos formas: X es mayor que Y e Y es mayor que Z, o forma simplificada podemos decir que X > Y > Z. Este es el motivo por el cual las matemáticas son tan solo un lenguaje simplificado con una herramienta para cada problema específico (por ejemplo 2+2= 4).

ORIGEN

La palabra «matemática» (del griego μαθηματικά mathēmatiká , «cosas que se aprenden») viene del griego antiguo μάθημα (máthēma), que quiere decir «campo de estudio o instrucción».Las matemáticas requieren un esfuerzo de aprendizaje o instrucción, refiriéndose a áreas del conocimiento que sólo pueden entenderse tras haber sido instruido en las mismas, como la astronomía. «El arte matemática», (μαθηματική τέχνη, mathēmatikḗ tékhnē) se contrapondría en esto a la música , «el arte de las musas», (μουσική τέχνη, mousikē téchnē), que sería un arte, como la poesía, retórica y similares, que se puede apreciar directamente, «que se puede entender sin haber sido instruido».​ Aunque el término ya era usado por los pitagóricos (matematikoi) en el siglo VI a. C., alcanzó su significado más técnico y reducido de «estudio matemático» en los tiempos de Aristóteles (siglo IV a. C.). Su adjetivo es μαθηματικός (mathēmatikós), «relacionado con el aprendizaje», lo cual, de manera similar, vino a significar «matemático». En particular, μαθηματική τέχνη (mathēmatikḗ tékhnē; en latín ars mathematica), significa «el arte matemática».

Función:

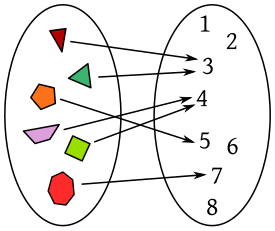
En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r (el valor del área es proporcional al cuadrado del radio, A = π·r²). Del mismo modo, la duración T de un viaje en tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que se desplace el tren (la duración es inversamente proporcional a la velocidad, d / v). A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.